Линейная зависимость и линейная независимость. Тема
Телеграм-канал магистратуры: http://t.me/ad_samgtu
Паблик ВК магистратуры: http://vk.com/ad.samgtu
Частные курсы. Telegram, WhatsApp, Viber: +7 (927) 74-69-502; VK: https://vk.com/id195593573
В чем состоит свойство линейной независимости набора векторов векторного пространства. И в чем состоит свойство линейной независимости.
--------------------------------
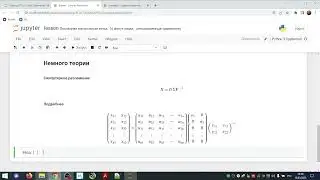
Линейная зависимость и линейная независимость — важнейшие понятия линейной алгебры. Для определения понятий линейной зависимости и линейной независимости вводится понятие линейной комбинации набора векторов, причем, если все коэффициенты в линейной комбинации нулевые, то такая линейная комбинация называется тривиальной (в противном случае — нетривиальной).
Свойства линейной зависимости и линейной независимости состоят в следующем:
1. набор векторов называется линейно независимым, если его обращает в ноль только тривиальная линейная комбинация.
2. если существует нетривиальная линейная комбинация, обращающая в ноль данный набор векторов, то такие векторы называются линейно независимыми.
Линейная зависимость и линейная независимость играют важную роль, так как при помощи этих понятий вводятся такие важнейшие понятия линейной алгебры как базис и размерность векторного пространства.
--------------------------------
Просмотрите видео по теме «Линейная зависимость и линейная независимость», затем перейдите к вопросам по теме «Линейная зависимость и линейная независимость», попробуйте самостоятельно решить данные вам задачи и, наконец, проверьте себя, просмотрев ответы на вопросы по теме «Линейная зависимость и линейная независимость».
--------------------------------
Тема «Линейная зависимости и линейная независимость»: • Линейная зависимость и линейная незав...
Вопросы по теме «Линейная зависимости и линейная независимость»: • Линейная зависимость и линейная незав...
Ответы на вопросы по теме «Линейная зависимости и линейная независимость»: • Линейная зависимость и линейная незав...